Angle Properties of Quadrilaterals

The quadrilaterals whose angle properties we will examine are either formed from isosceles triangles ( Kite, Rhombus, Square)  or from parallelograms ( Paralellogram, Rhombus, Rectangle, Square ) . So, before we begin;

• Angles Formed by Parallel Lines and Transversals
• Triangles ( Side - Angle Realationship ) 

Reading these two topics will greatly facilitate your understanding. 

Let's summarize;

 Angles Formed by Parallel Lines and Transversals

Using this property, we can determine the angle properties of parallelograms (including Rhombus, Rectangle, and Square).

Angles of Parallelogram ( Square, Rectangle, Rhombus, Parallelogram)

Let's draw the lines that are parallel to each other and their transversals.

Congruent Angles;

a//b and d is transversal of these lines. 

Also ;

e // d and b is transversal of these lines, so angles are congruent.

if we go on ;

a // b and e is transversal of these lines, so so angles are congruent.

Example 

Find the ungiven angles . 

Extend the parallel lines and the transversal.

Line d is parallel to line e, and line a acts as their transversal.

Line a is parallel to line b, and line e acts as their transversal.

Similarly, you can find angle properties in a square, rectangle, and rhombus. Because all of them are parallelograms.

if we summarize ; 

In a parallelogram, opposite angles are equal.

Angles of Kite

We know that a kite is a combination of two isosceles triangles.

And we know that in an isosceles triangle, the angles adjacent to the congruent sides are equal to each other.

But what about the other angles ?

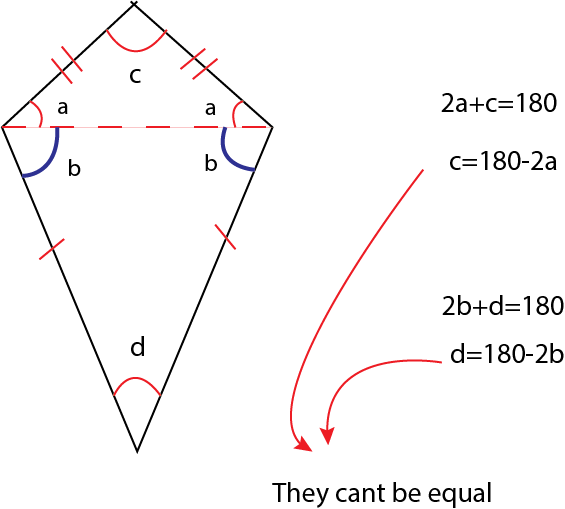
I find c by subtracting 2a from 180, and d by subtracting 2b from 180. Since I'm subtracting different numbers from 180, the results will be different. If we want the results to be the same, we need to subtract the same thing from 180. 

If a is equal to b, then since we are subtracting the same numbers from 180, c will also be equal to d.

Another Point of View

Imagine the upper triangle of the kite remains fixed while we adjust the lower triangle. If the lengths of the arms forming angle d decrease, angle d will increase, because the angles on the arms will decrease.

Imagine the upper triangle of the kite remains fixed while we adjust the lower triangle. If the lengths of the arms forming angle d increase, angle d will decrease, because the angles on the arms will increase.

This also shows us that c and d don't have to be the same. While c remains constant, we are able to increase and decrease d.

What is more ?

Triangles

Angles Formed by Parallel Lines and Transversals

Quadrilaterals

Geometry Index