Angles Formed by Parallel Lines and Transversals

Transversal : A  line that intersects two or more other lines. Lines don't have to be parallel, 

but we are going to look at a specific example of a transversal crossing parallel lines.Let's draw two lines parallel to each other.

When parallel lines are overlaid, they match exactly. Let's overlay the lines.

Let's draw a line perpendicular to these lines.

Now, let's spread the parallel lines apart again.

We obtain a line that intersects the parallel lines perpendicularly ( Transversal ).

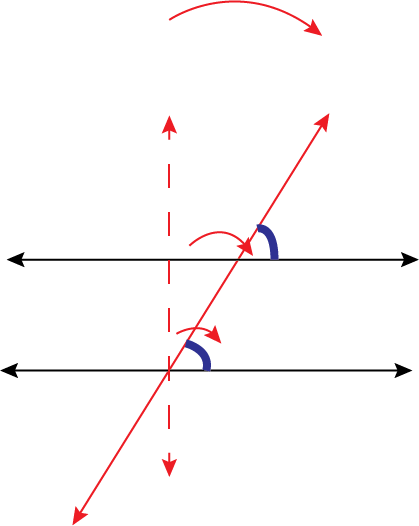
If we move the line to the right or left, the perpendicularity is disrupted. As the angle on top narrows, the angle below narrows by the same amount, so the angle below and the angle above become the same. (Initially, both were 90 degrees and both narrowed by the same degree.).

The angles formed above are replicated below.

Naming Angles

To name the angles, you need to know the concepts of the interior and exterior regions. The area between the two lines is called the interior region, while the other areas are called the exterior region. Angles are also named based on these interior and exterior regions.

Interior Angles : c, d, e, f

Exterior Angles : a, b, g, h

Corresponding Angles

When two parallel lines are cut by a transversal, the angles that are in the same relative position with respect to the parallel lines and the transversal are called corresponding angles. For example, if you have two parallel lines and a transversal intersects them, the top-left angle on the first parallel line and the top-left angle on the second parallel line are corresponding angles.

A key property of corresponding angles is that they are congruent (i.e., they have the same measure) when the lines are parallel and cut by a transversal.

Angle a corresponds to angle g = Above the line and to the right.

Angle b corresponds to angle h = Above the line and to the left.

Angle d corresponds to angle j = Below the line and to the right.

Angle c corresponds to angle i = Below the line and to the left.

Alternate Exterior or Alternate Interior Angles

Alternate Interior Angles: These are angles that are inside the two lines and on opposite sides of the transversal. When the two lines are parallel, alternate interior angles are congruent (i.e., they have the same measure).

Alternate Exterior Angles: These are angles that are outside the two lines and on opposite sides of the transversal. Like alternate interior angles, when the two lines are parallel, alternate exterior angles are congruent.

a and g Alternate exterior 

b and h Alternate exterior 

c and e Alternate interior 

d and f Alternate interior

Naming and remembering angles can be challenging, and things like which angle is equal to which can be a bit frustrating.

Fundamentally, what's important is which angles are congruent ( same measurement ) to each other.

Keep a close eye on alternate and corresponding angles.